今日算法07-斐波那契数列

一、题目描述

题目链接：https://leetcode.cn/problems/fei-bo-na-qi-shu-lie-lcof/

难易程度：简单

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

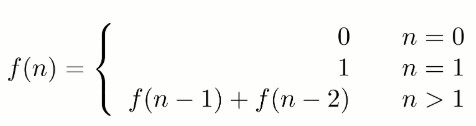
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

二、解题思路

动态规划

如果使用递归求解，会重复计算一些子问题。例如，计算 f(4) 需要计算 f(3) 和 f(2)，计算 f(3) 需要计算 f(2) 和 f(1)，可以看到 f(2) 被重复计算了。

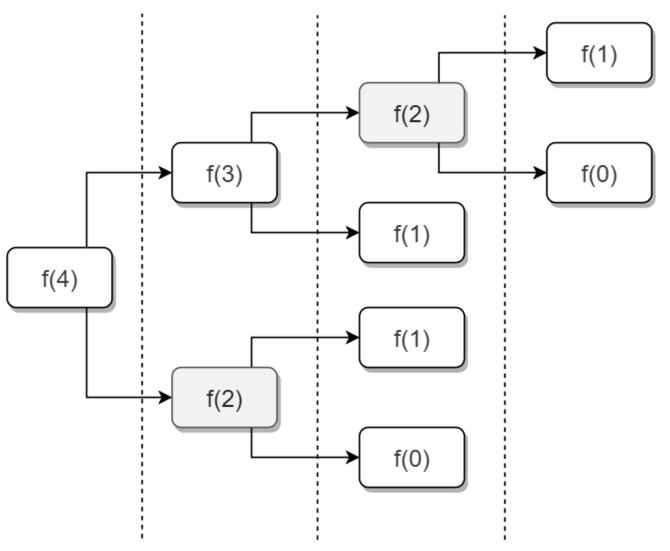
递归是将一个问题划分成多个子问题求解，动态规划也是如此，但是动态规划会把子问题的解缓存起来，从而避免重复求解子问题。

通常，动态规划解决问题的模板是：

1. 状态定义：opt[n], dp[n], fib[n]
2. 转移方程：opt[n] = best_of(opt[n-1], opt[n-2], …)
3. 初始状态
4. 返回值

本题套入模板，则是：

1. 状态定义：设 dp 为一维数组，其中 dp[i] 的值代表 斐波那契数列第 i 个数字。
2. 转移方程：dp[i+1]=dp[i]+dp[i−1] ，即对应数列定义 f(n+1)=f(n)+f(n−1) ；
3. 初始状态：dp[0]=0, dp[1]=1 ，即初始化前两个数字；
4. 返回值：dp[n] ，即斐波那契数列的第 n 个数字。

上面思路的代码实现如下：

public int Fibonacci(int n) {
    if (n <= 1)
        return n;
    int[] fib = new int[n + 1];
    fib[1] = 1;
    for (int i = 2; i <= n; i++)
        fib[i] = fib[i - 1] + fib[i - 2];
    return fib[n];
}

考虑到第 i 项只与第 i-1 和第 i-2 项有关，因此只需要存储前两项的值就能求解第 i 项，从而将空间复杂度由 O(N) 降低为 O(1)。

复杂度分析

时间复杂度 O(N) ：计算 f(n) 需循环 n 次，每轮循环内计算操作使用 O(1) 。

空间复杂度 O(1) ： 几个标志变量使用常数大小的额外空间。

三、代码实现

public int Fibonacci(int n) {
    if (n <= 1)
        return n;
    int pre2 = 0, pre1 = 1;
    int fib = 0;
    for (int i = 2; i <= n; i++) {
        fib = pre2 + pre1;
        pre2 = pre1;
        pre1 = fib;
    }
    return fib;
}

推荐阅读

• 今日算法06-用两个栈实现队列

封面

今日算法系列，题解更新地址：https://studeyang.tech/2023/0721.html