今日算法08-矩形覆盖

一、题目描述

题目链接：牛客网

难易程度：简单

我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形，总共有多少种方法？

二、解题思路

动态规划

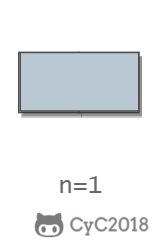
当 n 为 1 时，只有一种覆盖方法：

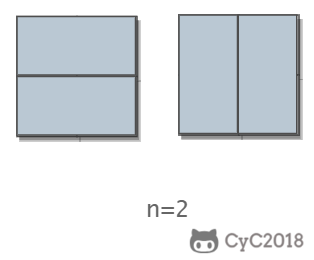
当 n 为 2 时，有两种覆盖方法：

要覆盖 2*n 的大矩形，可以先覆盖 2*1 的矩形，再覆盖 2*(n-1) 的矩形；或者先覆盖 2*2 的矩形，再覆盖 2*(n-2) 的矩形。而覆盖 2*(n-1) 和 2*(n-2) 的矩形可以看成子问题。该问题的递推公式如下：

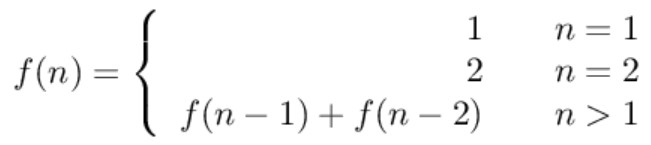
也就变成了斐波那契数列问题，参考：今日算法07-斐波那契数列

复杂度分析

时间复杂度 O(N) ：计算 f(n) 需循环 n 次，每轮循环内计算操作使用 O(1) 。

空间复杂度 O(1) ： 几个标志变量使用常数大小的额外空间。

三、代码实现

public int Fibonacci(int n) {
    if (n <= 1)
        return n;
    int pre2 = 0, pre1 = 1;
    int fib = 0;
    for (int i = 2; i <= n; i++) {
        fib = pre2 + pre1;
        pre2 = pre1;
        pre1 = fib;
    }
    return fib;
}

推荐阅读

• 今日算法07-斐波那契数列

封面

今日算法系列，题解更新地址：https://studeyang.tech/2023/0724.html